
Decisive Advantage but Lost on Time?
Losing on time in mate in X scenarios in 1+0 bullet gamesBefore reading this post
The games in this analysis were lichess-annotated 1+0 bullet games from April 2023. More about the data can be found at the lichess open database. Lichess does not annotate all their games in the database file, only a few games are annotated. Especially, 1+0 games with annotations compose less than 5% of the total 1+0 games. Annotations are done using Stockfish according to lichess. The analysis will not dig deeper into questioning the authenticity of the analysis. This post was supposed to be part of the last post but I found some issues in my analysis and needed time to fix my pipeline.
Categorizing "mate in X" games
Given that a "mate in X" occurred in a game, we can classify games using a combination of 3 vocabularies: "blundered mate / found mate", "won / lost", and "normally / on time". The occurrence of "mate in X" means the evaluation before the move was not a "mate in X". To give some examples:
- White moved, evaluation changed from 0.01 to "#7", and white checkmated black. This would classify as White "found mate" + "won" + "normally"
- Black moved, and the evaluation changed from 0.01 to "#7", but black won on time. This would classify as Black "blundered mate" + "won" + "on time".
The following is the distribution given this classification method.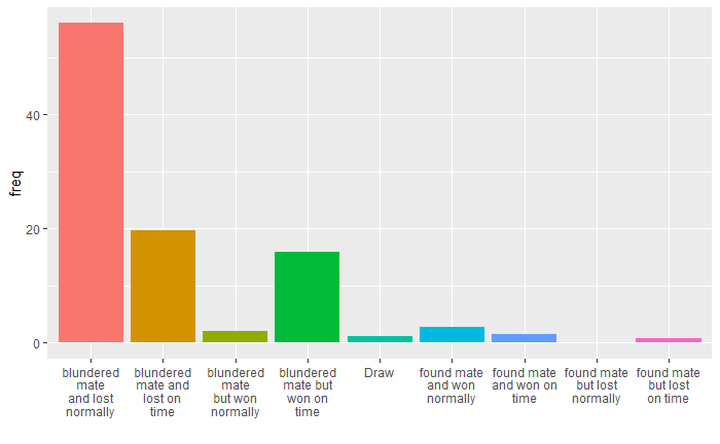
We can see that most blundered mates will result in losing normally or on time. This account for more than 70% of the games including a "mate in X". However, there is a significant amount of games where a side blundered mate but won on time. This will be the focus of today's post.
Mate in X but losing on Time
Most people who play chess probably can find a mate in 1 if it happens in their game. Or do they?
The graph might be hard to interpret but it is a distribution of categories given a mate in X. For instance, given mate in 1, most games classify as "blundered mate and lost normally". So most lichess bullet players have a good time punishing other players for blundering mate in 1. However, as X grows, the proportion of "blundered mate and lost normally" diminishes. The proportion of "blundered mate but won on time" starts to grow up.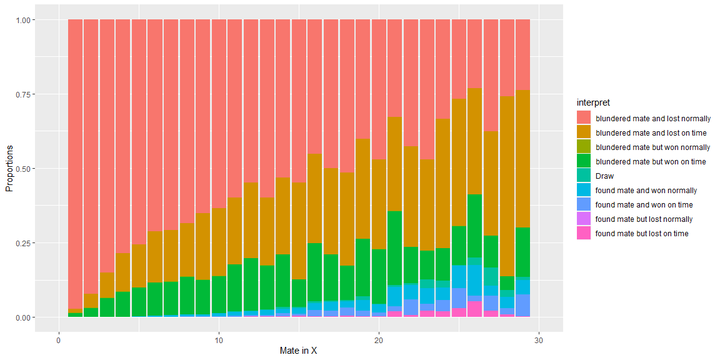
So what mate in X are people missing and why?
The below graph shows the distribution of mate in X distribution and the mate in X that happened in the games where a player blundered mate but won on time. We can see a clear difference. The proportion of mate in 1 and 2 drops significantly. The statistics for each distribution are as follows:
| Types | Mean | STD | Q1 | Q2 | Q3 |
|---|---|---|---|---|---|
| All Games | 6.10 | 5.55 | 2 | 5 | 8 |
| Blundered mate but won on time | 6.93 | 5.47 | 3 | 6 | 9 |
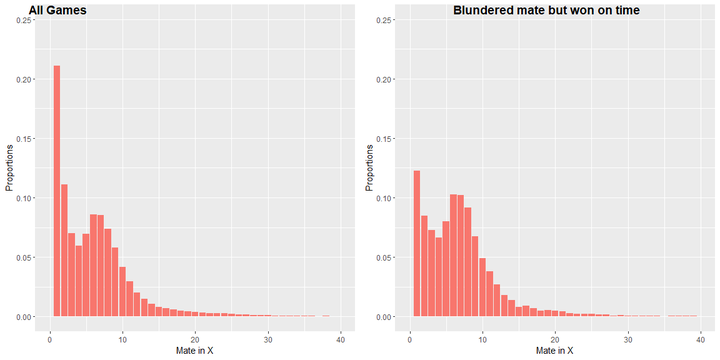
We should also consider the time the player has when they face this situation. For example, most people will not find a mate in 11 given 1 second on the clock. From the graph below we can actually see that the proportion of Time less than 20 seconds is large and mate in 6+ happened a lot in that time frame. Maybe practicing mate in X puzzles with low time might help in improving these players.
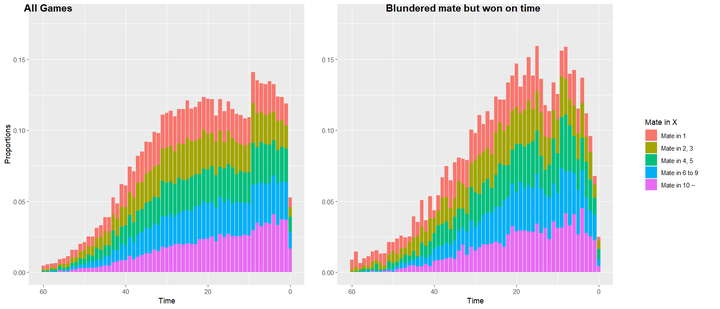
Time management
We should also dig deeper into the time management differences between the two players. Below is the distribution of the Time difference (player who won - player who lost) when the mate in X blunder happened. On average, the blundered side was 8 seconds ahead on the clock when they blundered.
- Mean = 8.66, STD = 8.68, Q1 = 2, Q2 = 8, Q3 = 14
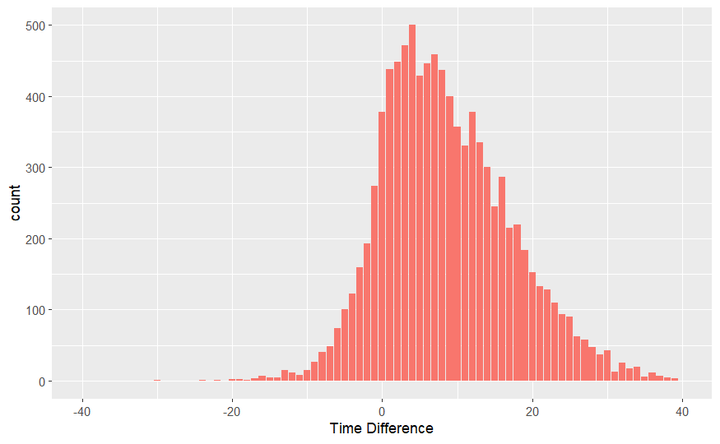
The Time difference continued after the blunder happened. We would assume the side that blundered would take more time to come back into the game but the lead in time doesn't seem to evaporate.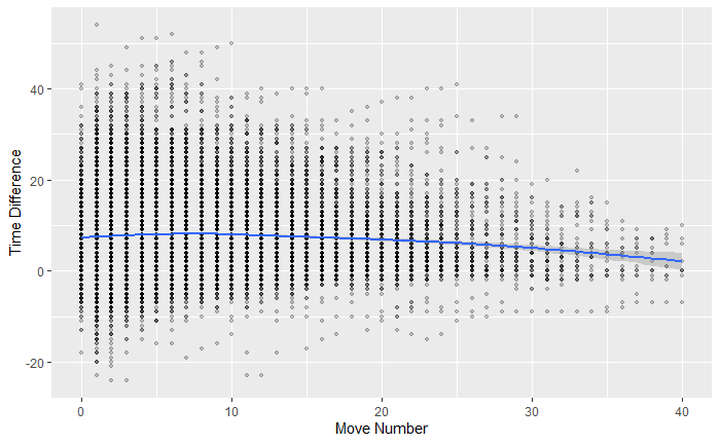
It turns out, that the losing player spends more time on every move even after the mate in X situation.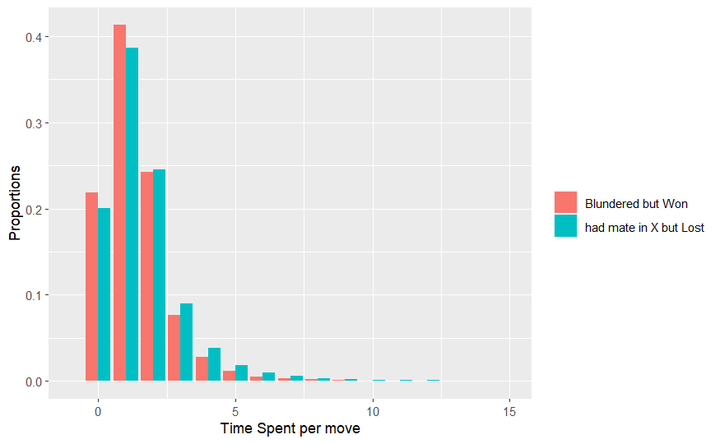
In every type of move, the side that lost on time spent more time. However, this may be due to the playing style of such players. They might spend more time to get the decisive advantage and are more careful when trying to deliver checkmate and during that process, they might be losing on time. This is a topic of its own and I just wanted to share some statistics.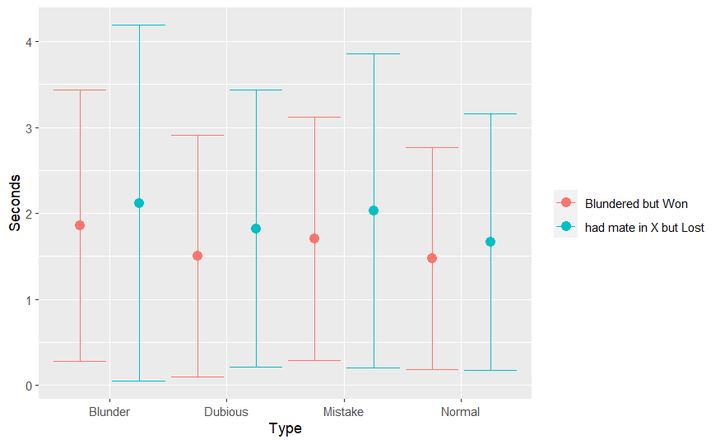
Other Visualizations
This is the type of move given the time spent on the move. For instance, given 0 time spent on the move for players who blundered but won, 75% were normal moves. We can see that the proportion of normal moves is higher with lower Time spending. This may be due to opening and some obvious, non-losing safe moves. The proportion of normal moves is generally lower in both of our subjects of study. This may be due to the complicated middle game in which mate in X happens. Probably there are a lot more moves the engine would say is a "mistake" or "blunder".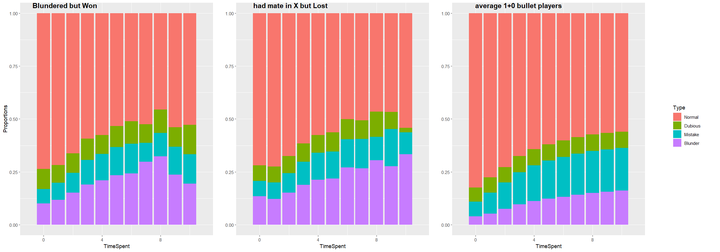
Future posts
If there are any topics you wish me to analyze, I would love to know. Feel free to discuss the analysis in the comment. Thank you for reading my post.
You may also like
 oortcloud_o
oortcloud_oWhich openings are related?
simulating opening connectivity graphs with known techniques GM NoelStuder
GM NoelStuderThe Best Chess Opening
One of the most frequently asked questions is: What is the best chess opening? In the span of one we… oortcloud_o
oortcloud_oHow long is an opening?
A new approach on where opening ends oortcloud_o
oortcloud_oLinking top players based on openings
Using relatedness network on opening choices of top grandmasters oortcloud_o
oortcloud_ochess heatmaps but better
you will not regret oortcloud_o
oortcloud_o